
背景简介:
NKN近期宣布了Wolfram Mathematica创始人兼首席执行官Stephen Wolfram博士加入NKN担任顾问。Stephen Wolfram同时也是“一种新科学”(New Kind of Science)(NKS)的作者; Mathematica创建者,Wolfram | Alpha和Wolfram语言的主设计师。鉴于其对元胞自动机的开创性发现,他参与到NKN项目是一个很自然的选择。我们最近与Stephen会面,向他详细解释了NKN的工作原理以及它与其他区块链应用的不同之处。
在最近的一次访谈中,NKN首席技术官张逸伦博士(YZ)和Stephen Wolfram(SW)探讨了如何使用Wolfram | One仿真并让NKN网络可视化,以及基于NKS原理的元胞自动机创新共识算法的细节,和如何在异步情况下进一步提升共识算法。
点击下面的Wolfram notebook文件可以访问其中源码并与其进行图形可视化的交互(某些功能需要Wolfram语言版本12):
https://www.wolframcloud.com/objects/outreach/Published/nkn-stephen-wolfram-interview
以下是访谈实录:
NKN是什么?
SW
项目名称NKN(New Kind of Network)(对应Stephen Wolfram 的科学巨著NKS-译者)确实激起了我的兴趣!当我看到你们在NKN白皮书的前两个参考文献中列出了我的名字时,我就知道我是真有必要搞明白你们在做什么。所以我期待了解关于NKN的所有信息。
据我理解,你们是希望构建一个基于互联网上的通讯网络,可以通过共享大家的计算机来路由数据,并使用数字通证对其进行经济补偿,我的理解对吗?
YZ
是的,就人们如何使用这个网络而言,您的理解是对的。但我们同时也在做一些其他事情,而这与NKS的观点密切相关:我们正在试图创造一种新的共识机制,即通过局部规则而非全局定义的方式来达成共识。所以我们在搭建一个更好的传输网络的同时也在构建一个更好的区块链系统。
SW
这听起来非常雄心勃勃。酷。
数据包如何通过网络传输?
SW
好吧,让我们来了解一下它是如何运转的。所以,我想在NKN网络上做的最基本的工作就是将数据包从一个地址发送到另一个地址。NKN网络由很多节点组成的-这些节点是在其上运行NKN路由软件的计算机。NKN网络的一个具有代表性的目标是弄清楚如何从节点向节点发送数据包以使其到达目的地。
我想因为该协议很大程度上同时具有密码学和区块链属性。根据我的理解,NKN实现了两件大的突破。首先,它可以让通信更安全。其次,它提供了一种验证哪些计算机正在传输数据包的方法,并可以通过加密货币对这种网络资源共享行为进行支付或激励。
YZ
是的,这儿有一个典型的数据包如何在整个网络进行传输的路径示例:
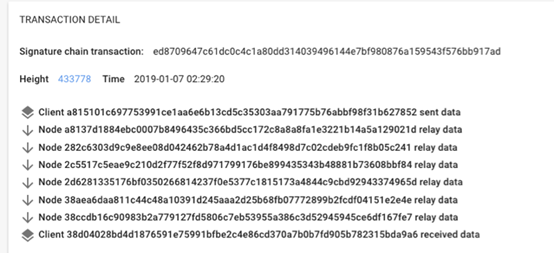
(NKN测试网中的签名链示例)
SW
那么是什么决定了转发路径的中继节点数量呢?
YZ
嗯,基本上它大约是NKN网络中所有节点数量对数的一半,其中对数的基数与每个节点的虚拟邻居的数量有关。
SW
虚拟邻居是什么意思?我想你最终是希望数据包在底层互联网络中物理上接近的节点之间进行跳跃式传播。但我猜和你刚才说的“虚拟邻居”是不一样的?
YZ
是的,虚拟邻居是NKN地址空间中的一种邻居关系。每个NKN节点会被随机分配一个长度为256比特的唯一标识符。然后我们想要的是两个不同的功能,从某种意义上来讲是有些对立的。一方面,我们希望能够尽可能地用最直接的路由来传输数据包。另一方面我们希望它足够安全的完成这一点 - 为了实现这一目标,我们在数据传输路径中添加了一定的随机性,以防止一些恶意者破坏或操纵它。
这个机制在效率和安全性之间取得了很好的平衡。我们通过扩展和提升Chord DHT(弦状分布式哈希表)来实现这个平衡。
SW
好,那么它们是怎样运行的呢?最终是否有基于NKN地址的固定距离度量?
YZ
是的。给定任意两个NKN地址a和b,它们之间的距离为(b-a)mod2²⁵⁶。
SW
好的,我想我必须在这里开始引入代码。所以让我们做一个简单的案例,用2¹⁶而不是2²⁵⁶。假设我们有50个这种类型的地址:

现在让我们定义一个函数来寻找最近的邻居:

好啦,所以使用该函数,我们可以找到10个最近的邻居,比如我们列表中的第一个节点:
![]()
所以这些就是您正在使用的虚拟邻居吗?
YZ
这是其中一种类型的虚拟邻居。但是还有另外两种类型。如果我们只是使用了第一个类型,那么一些数据包将花费相当长的时间来进行传输。事实上,如果我们共有k个邻居和n个节点,那么它可能是n / k步。
所以我们添加一些中间的“转发邻居”来帮助我们更快地传输数据包。这些转发邻居基于将2 ^ i添加到每个现有节点的地址,然后查看哪些节点具有最接近该节点的地址。
SW
让我看看我是否已经理解了。假设我们从之前的列表中的第一个节点开始。然后我们将2 ^ i(mod2¹⁶)添加到其地址:
哦,如果i很小,邻居节点的距离不足以到达下一个节点怎么办?
YZ
我们只需选择不重复的节点即可。
SW
啊,所以它会是:
![]()
YZ
好的,还有一步。我们将原节点的最近邻居称之为“后继”节点。第三类虚拟邻居是前驱节点,它们就像是后继节点和转发节点的反转。
顺便说一句,当我们找出后继节点时,如果n是节点总数,我们有大约2 log(n)个后续节点。这样即使有很多网络中的节点同时突然消失,这些后继节点依然能让整个网络保持很好的健壮性。
SW
做一个实验看看这一切是如何提高路由效率的应该会很有趣。但是答案是什么呢?
YZ
基本上一个典型的数据包需要O(log(n))跳进行传送。如果你只使用了后继节点,那就是O(n)步骤。你实际上可以证明O(log(n))结果,因为通过我们的设置,每一跳都能有效地将距离减半…
SW
我们为什么不尝试用软件来生成一个图形?首先,让我们按顺序围绕一个圆圈排列所有2¹⁶节点。然后让我们看看第一个节点连接到哪些节点:
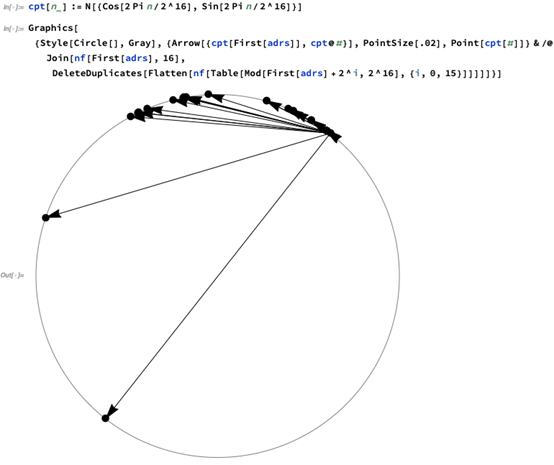
因此,当我们启动它的时候,第一个节点连接到了一堆节点,这些节点在距离上大致以指数级逐渐地变远分布。
再让我们看看这个设置对整个节点网络的作用,比如我们随机的选择100个节点。为了了解正在发生的事情,也许我们可以先看看如果我们将每个节点连接到更多的邻居会发生什么:
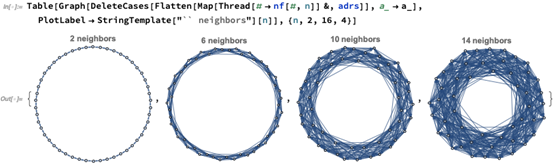
我们确实可以在这里看到节点排列的环形结构 - 这意味着信息从一个节点到另一个节点可能需要很长的时间。
但现在让我们来看看用2 ^ i的“转发节点”而不是最近邻居时会发生什么:

现在让我们将这些转发节点与最近的16个邻居组合起来:

很显然,这里的连接情况要好得多。通过绘制每个节点到另一个节点所需的中转节点数的直方图,我们可以了解连接提升了多少。这里比较只有邻居,只有转发节点,以及两者组合的情况:
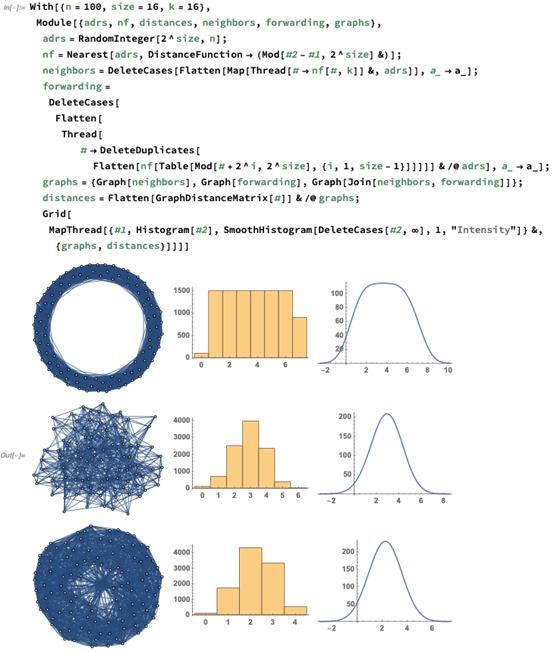
YZ
是的,对于两者组合的方式,网络距离的分布符合高斯分布。
SW
我想我现在可以“看”到为什么这个算法(ChordDHT- 译者注)的名字中有“弦”(Chord)这个词 --它包含很多通过圆环进行的连接。
好的,但是从特定节点开始的数据包,它实际上是如何将自己路由到目的地的呢?
YZ
它所要做的就是获取它当前所在的地址,然后传递至距离目的地最近的虚拟邻居中。基本上在每一步它离目的地的距离在NKN地址空间中将大致减半。
记录发生了什么,并就此达成共识
SW
好的,刚才我们已经谈了一些关于数据包如何通过NKN网络进行传输的问题。下面让我们来谈谈你们在区块链方面所做的创新。据我了解,你们正在尝试在数据包的报文头中创建“签名链”作为数据包如何在全网中进行传输的一种安全“鉴定证书”。
YZ
差不多。实际上,对于一系列连续的数据包,可以用单个的签名链。
SW
好的,那么什么信息会被放入签名链中呢?
YZ
它基本上是一系列数字签名和节点地址的集合。在每个步骤中,它记录将要访问的下一个节点的地址,以及与先前数字签名组合产生的新的数字签名。
SW
所以在代码中会是这样的:
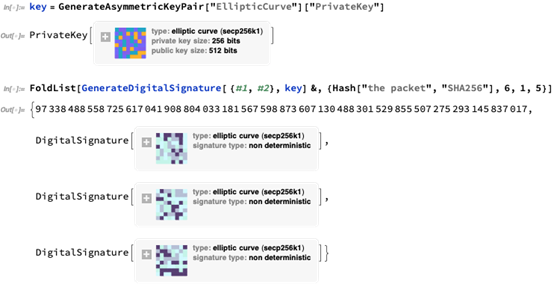
YZ
是的,稍有区别是我们用了不同的椭圆曲线。
SW
很好。但是我想这将引入另外一个区块链(指签名链构建的链状结构-译者注)?
YZ
是的,这个区块链可以用作人们共享自己的节点中继数据包的记录凭证。
这儿也将是“一种新科学”(NKS)的用武之地。因为这里我们需要达成共识来决定那些区块应该被加到NKN的区块链上来。
SW
好。所以让我明白这一点。在像比特币或以太坊这样的经典区块链中,您可以使用工作证明(proof of work)来决定谁添加下一个区块。换句话说,你基本上使用的是我称之为计算不可约束性的东西 -以解决哈希问题这种特定的形式 - 为决定谁可以添加区块设置这样一种计算力竞争。它的工作方式是通过矿工竞争来赢得这场比赛,并且一旦他们中的一个到达终点线(指满足计算要求-译者注),他就会将结果广播到网络。当然,这整个事情浪费了巨大的计算资源和电力。
我猜这就是为什么一些更现代的区块链试图转向“股权证明”(POS)而不是工作量证明的原因,认为持有更多加密货币的节点应该有更大的机会来确定下一个区块应该是什么。实际上是怎么做的呢?
YZ
几年前,人们只是让持有加密货币更多者解决相对更简单的问题。但是现在有一种不同的方法,它是基于直接在节点之间形成共识。
第一步是让所有节点就哪一个节点成为下一个区块的提议者达成一致。
SW
所以我想这意味着他们实际上必须使用类似于“通过电话抛硬币”的协议…
YZ
是的。虽然不同的区块链使用不同的版本。
SW
好的,但是一旦每个人都同意谁将提出下一个区块,该区块是如何被验证的?
YZ
它需要再次达成共识。但现在它通常只是“验证节点”之间的共识。如果这些节点间达成共识,则将区块添加到区块链中。
SW
好吧,但是你们如何在NKN中建立共识呢?我感觉这儿就是NKS真正需要引入的地方。
YZ
是的。我们所使用的最重要的就是我们称之为MOCA(Major vOte Cellular Automata ):“多数元胞自动协议”的共识机制。
SW
嗯,好吧。经过这么多年研究元胞自动机,我最好能够先向人们解释什么是元胞自动机。让我们从最简单的版本开始:具有两种颜色的一维元胞自动机。我们刚刚获得了一行黑白色的细胞,并且每一步我们都会根据上一步细胞的颜色更新特定细胞的颜色。以下是我们可能使用的规则的一个示例:

我们从单个黑色单元格开始启动,下图是我们根据上面的规则得到的变化结果/范式:
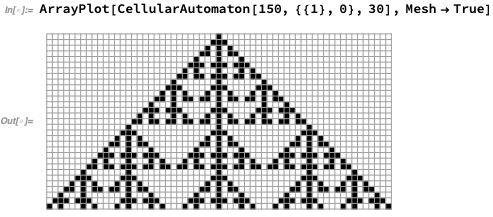
这结果并不总是那么的规律(指显示的有一定规则性-译者注),但我们先不谈这个,至少目前还不用。
那么什么是“多数投票”规则呢?在我不久前发明的编号方案(指Stephen Wolfram在NKS中对各种元胞机规则进行的分类编号-译者注)中,它的规则编号是 232:

只要邻域中有多个黑色单元格,则下一步结果就是黑色。否则它就是白色的。
那么如果我们从第一行里80%的单元格是黑色开始会发生什么呢?被黑色占主导地位的地区很快就会变成黑色 - 但进程就会被卡住:

当然这是一种最简单的多票数规则:
![]()
如果我们也允许下一个最近的邻居,我们将得到如下规则:
![]()
事情再次陷入困境:

所以,你可能会问,有没有办法真正达成共识,因为当初始条件下有超过50%的黑色单元格时,整个系统最终将变黑,而当这个初始值减少到多少时,它会变成白色?实际上,这是物理学中经典的相变情况。事实证明,元胞自动机是一个非常简单的例子。这一点在我的NKS书中也讲的特别清楚。
如果我们从70%黑色开始,每个单元很快就会变黑:

如果我们从70%白色开始,一切都会变成白色:
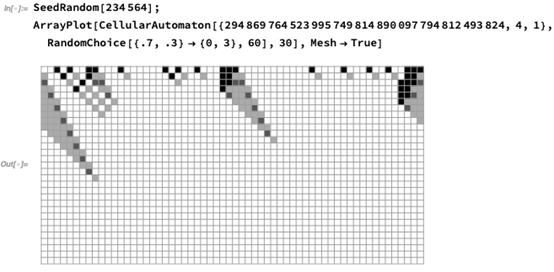
请注意,有一些三角形突出,因为系统“决定”主导色将是什么。那么如果它真的接近50%黑色,50%白色时会发生什么?这是一个52%黑色的案例:

它最终“决定”共识值是黑色的,但需要一段时间。实际上,如果选取的ε偏离50比50(即一半黑一半白-译者注)的话,则需要大约ε^ɣ步,这里的ɣ是一个常数。在50比50的点上人们在统计物理学意义上有一个“临界点”,系统会花费无限的时间“决定做什么”,在此过程中产生一个完整的部分决策嵌套结构:

在这个特定的规则中,“共识决定”是一个非常有条理的 - 而且,人们可能会说,这是一个缓慢的过程。事实证明,还有其他规则可以产生一些有效的随机性,并且让“决策”可以更快地进行,尽管略有概率上的不同。
好的,但在NKN的实际网络中,它不仅拥有一维单元格, 它实际有一个网络。让我们通过查看二维的情况来更好的接近它。
让我们尝试一个纯粹的多数规则,对最近的邻居进行操作。这是规则,灰度级显示邻域中所有单元格的总值:

如果我们从70%的黑色开始,会发生什么。它收敛于“大多数是黑色”,但存在一些小的“瑕疵”:

在三维空间里(空间的两维,时间一维)这是正在发生的事情(这里显示30%黑色):

这是“从边缘”观察并计算平均值:

这是一个有更多单元格的例子,再次显示了一定数量的“瑕疵”:
如果我们使用更多的邻居连接数,会发生什么:
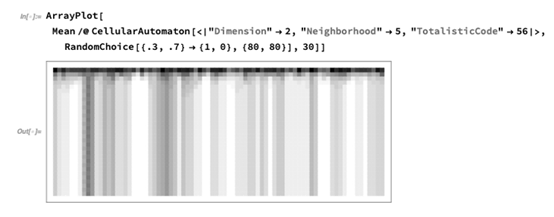
如果我们使用稍微再多一点的单元格,会发生如下的情形:

如果在本地投票时包含更多的周边单元格,则残留的“瑕疵”会减少:

这是初始值是30%黑色的“侧面”视图:

好的,但是有没有更好的规则,可以不留下“瑕疵”呢?这里有一个将这个任务最终完成的不错的规则,尽管它需要一些时间来达成最终决议:

请注意,尽管它是多数票规则,但有一些变化。经过5个步骤后,它还没有“决定”做什么:

如果我们采取更多步骤,看看会发生什么:

这是“侧视图”:

好的,那网络的情形会怎么样的呢?不要让所有节点都集中在一个数组中,让我们假设它们在一个NKN网络中连接起来。

(一个完全连通的图将在一步里收敛。)
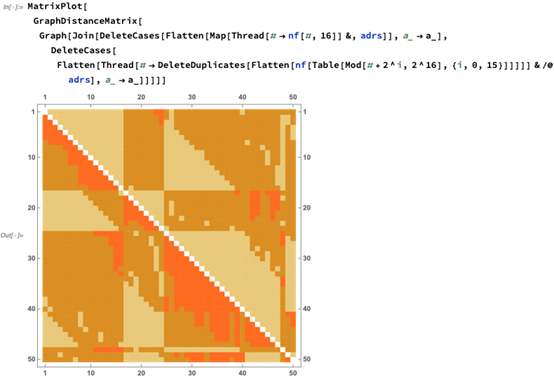
如何处理恶意节点?
YZ
现实世界中的一个复杂因素是,并非每个节点都会正确运行我们所指定的共识算法。他们有可能运行算法被修改的后的恶意节点,也有可能是故意试图搞乱系统。
SW
这就像有一个有概率属性的元胞自动机,其中给定细胞有一定的概率根据不同的规则得到更新。您是希望恶意节点固定不动,还是可以随机移动?
YZ
首先,让我们假设一个节点是好的,或者是恶意后保持永远不变。稍后,我们可以考虑如果节点可以更改会发生什么。
我们考虑的攻击模型如下。 N个节点中有M个恶意节点。攻击成功的定义是恶意节点可以强制共识收敛到少数而不是大多数诚实节点的初始状态。恶意节点可以向其邻居发送任意投票,而不是遵循共识协议,但是他们无法更改其邻居,因为我们选择的拓扑是可验证的。我们考虑这种攻击模型的原因是,如果攻击者可以强制诚实节点收敛到少数群体状态,那么他们基本上可以控制共识结果,或者让它收敛到任何状态,或者让它根本不收敛。
我们发现攻击是否成功取决于两个参数:系统中有多少恶意节点,诚实节点初始状态的分布。例如,如果所有诚实节点最初处于相同状态,那么我们需要相当多的恶意节点,实际上是N / 3左右,以迫使所有诚实节点改变他们的意见。但是,如果诚实节点具有处于平衡的初始状态,那么只有少量恶意节点就足以打破任何方向的平衡,从而控制共识结果。我们称这样的属性为有条件的BFT(拜占庭容错) - 也就是说,共识是否是BFT取决于初始条件。我们最终使用系统设计的其他部分来帮助网络保持在BFT区域。
使网络变得高效
SW
因此,如果要防止恶意节点扰乱网络,则需要随机化路由。就发送数据包的最短和最快路径而言,这样做的效率似乎并不高。
YZ
确实有一些效率和安全之间的权衡。但是,我们实际上可以使NKN路由比当前的Internet缺省路由更好。 NKN节点之间的每个链路都知道它的ping时间,因此从给定节点,您可以选择具有最低延迟的节点。
此外,您可以在发送方和接收方之间创建多个并发NKN路由。这样,您甚至可以聚合所有虚拟路径的带宽。最近我们做了一个网络加速器的原型,并通过这样做实现了167% - 273%的速度提升。文件越大,增强效果越好。它告诉我们,Web下载的瓶颈既不是内容服务器也不是用户的宽带上网线路,而是在默认网络路由路径的中间。
应用
SW
好的,所以如果所有这些按计划运行,你们能用它做什么呢?看起来它可以创造比Bit Torrent更好的版本,对吗?
YZ
我们可以让许多应用程序无需任何集中式的服务器即可直接通信。例如,一些最直接的应用包括像即时通讯,网络代理和中继,实时视频流传输和文件共享,动态内容分发网络(CDN)等。
理论上,任何需要用户到用户端通信的应用程序都可以基于NKN网络构建。因此,我们相信NKN的潜力是无限的,我们真的很高兴您以及Wolfram Research团队可以帮助我们一起实现这个雄伟的目标。
结论
这次访谈的关键点:
1) NKN使用基于Chord DHT的新型分组路由协议和“弦”式的覆盖网络,可以用Wolfram | One模拟仿真和可视化。这对所有区块链项目都有启发意义:协议设计人员现在可以使用Wolfram | One的强大工具来数学证明,模拟和改进算法,而不需要在运行大规模测试网络时浪费成千上万美元的云计算成本。
2) NKN正在创建一种新的共识算法,它基于NKS原理和元胞自动机规则,极其高效和具有极强的扩展性。通过竞争哈希能力的传统共识算法,是Stephen Wolfram在NKS中发现的计算不可约束性原则的一个有趣且令人惊讶的转折。并且在30年前就被预见了。
3) Stephen Wolfram相信通过NKS的原理和方法进一步探索计算空间,我们可以为NKN和异步共识系统不断改良共识算法。通过与NKN的合作,我们可以帮助提升整个区块链技术行业的水平。
关于Stephen Wolfram博士

Stephen Wolfram博士
Stephen Wolfram博士是Mathematica,Wolfram | Alpha和Wolfram语言的创造者,NKS的作者,同时也是Wolfram Research 公司的的创始人兼CEO。在近四十年的时间里,他一直是计算科学开发和应用的先驱 - 并且拥有许多科学、技术和商业领域的发现,发明和创新。了解更多信息请浏览:
stephenwolfram.com.

关于NKN
NKN是一个完全去中心化,基于网络传输量工作证明,可支持千万级规模节点共识的区块链系统。由NKN所构建的这样一个有经济模型所驱动,社区共建共享的新型点对点网络,为开发者提供了一个开放、便捷、高效和安全的网络连接传输平台。基于NKN开发的各种应用将给终端用户带来各种全新的网络体验。

主页: https://nkn.org/
邮箱: [email protected]
Telegram: https://t.me/nknorg
Twitter: https://twitter.com/NKN_ORG
Medium: https://medium.com/nknetwork
Linkedin: https://www.linkedin.com/company/nknetwork/
Github: https://github.com/nknorg
Reddit: https://www.reddit.com/r/nknblockchain
Discord: https://discord.gg/yVCWmkC
